日常整活之模拟sin曲线

本文章内容已过期，相关内容并不准确。

前情提要

最近也是放寒假了，自己一个人在家也挺寂寞，所以总想着干点什么打发一下时间🤓

游戏的话，玩多了也会觉得腻，况且我既不是肝帝又不是氪金选手😨

于是在一个月黑风高的晚上（bushi），我在床上思索着，我们现在所熟知的三角函数能不能用一些简单的函数去模仿呢🧐

我就决定从最基础的$\sin$函数开始…

理论部分

一说到$\sin$函数，上过中学的朋友可能再熟悉不过了，它的图像是这样的：

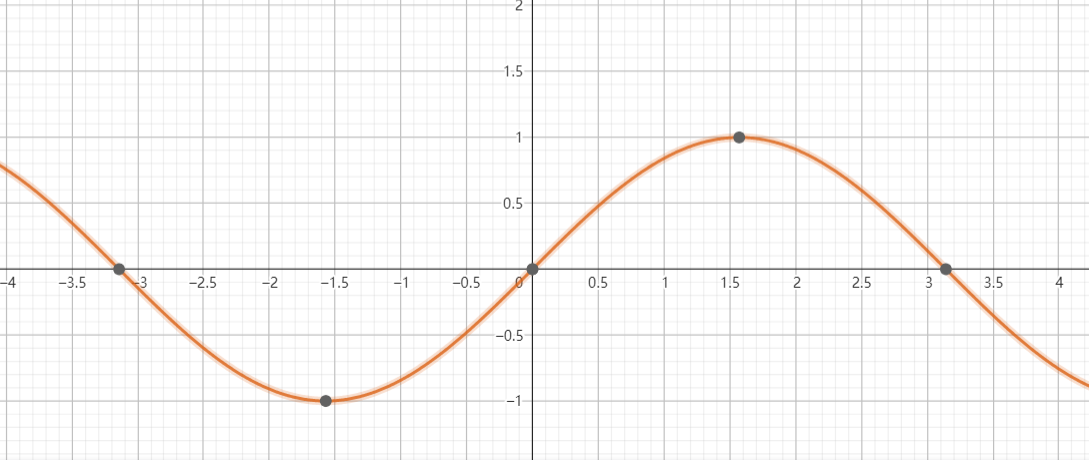
可以看到，它的形状像不像多条连起来的抛物线？🧐

而一想到抛物线，我们就能联想到初中学过的二次函数，二次函数的形式看起来应该是这样的：

$$f(x)=ax^2+bx+c\qquad(a\ne0)$$

那根据初中学过的二次函数基本性质可以知道，当系数$a>0$时,抛物线的开口是向上的，而当$a<0$时，抛物线的开口向下🧐

而我们又知道，$f(x)=(-1)^x$这个函数，当$x$为偶数时结果为正，当$x$为奇数时结果为负，那是不是可以通过这个原理改变抛物线的开口呢？

但是我们又知道，一般二次函数的图像是无法做到上图中类似$\sin$函数的效果的，是因为二次函数的曲线只有一段，而没有类似上图中那样波浪线的效果，那我们该如何实现呢？

先别急，我们来看一道小学题目找找灵感

小亮手上戴有一长串的彩色珠子，按红、黄、蓝、绿、紫五种颜色排列，共有100颗珠子。请问第73颗是什么颜色？

看到这个题，肯定大家心理已经有了答案，就是计算73除以5的余数，得出来是3，那么就是第三种，答案就是蓝色

那这个题和我们今天整的活有什么关系呢？刚才说到曲线的不连贯问题，我们是否可以利用上面的余数原理，对$x$进行取余，然后让他能够像波浪一样？

那我们先用以下这个函数做个小实验：

$$f(x)=x^2$$

可以看到这个函数是一个基本的二次函数，那如果我们把其中的$x$进行取余会变成什么呢?

$$f(x)=(x\mod 1)^2$$

注：mod是取余的意思

这里就随便对1进行取余了，然后效果就变成了这样:

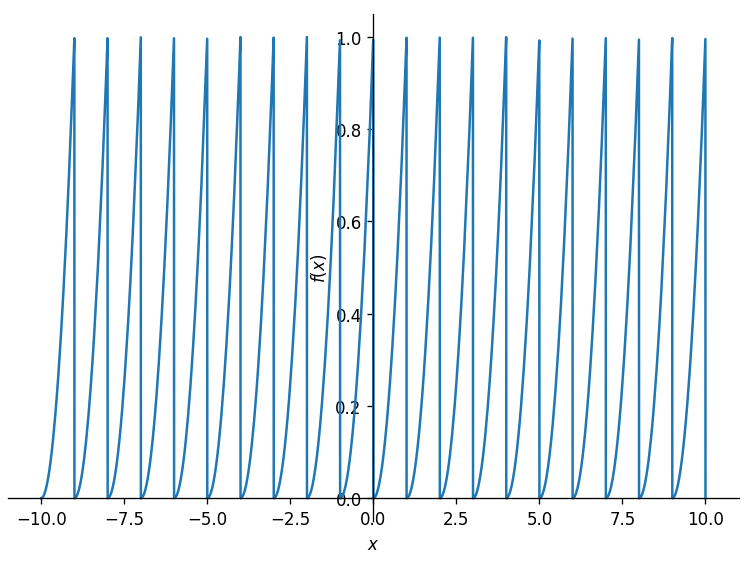
可以看到和普通的二次函数图像有了极大的不同，而且具有了类似波浪一样的重复，但是还是没有做到类似$\sin$函数那样一上一下的效果，怎么办呢？

还记的之前提到的$f(x)=(-1)^x$吗，如果在前面改造后的函数上再乘上$(-1)^n$是不是就能实现一上一下的效果了？

但是事情并没有这么简单，$(-1)^n$的$n$是多少呢？那就得看在第几个周期了，那周期是多少呢？我们之前取余数是取的$x$除以1的余数，那周期不就是$x$除以1的结果取整数部分吗？那就可以记作$\lfloor\frac x1\rfloor$

于是理论成立了，我们来改造一下之前的函数，改造后如下：

$$f(x)=(-1)^{\lfloor\frac x1\rfloor}(x\mod 1)^2$$

既然函数搞出来了，那就来看一下效果：

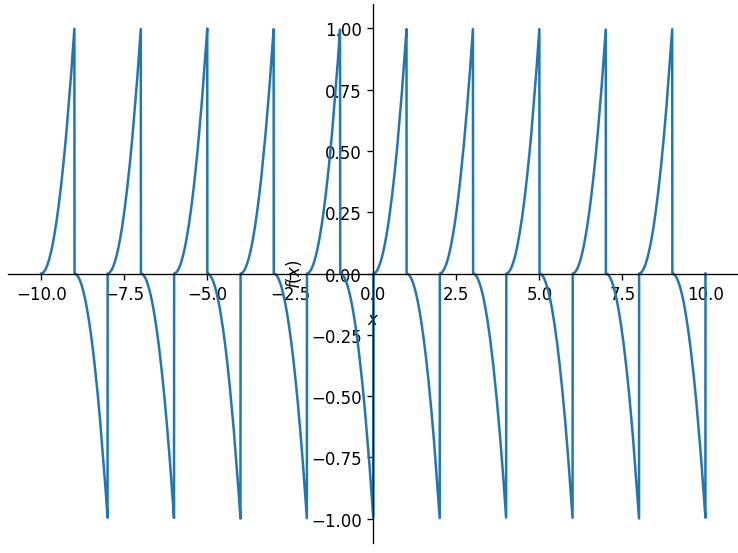
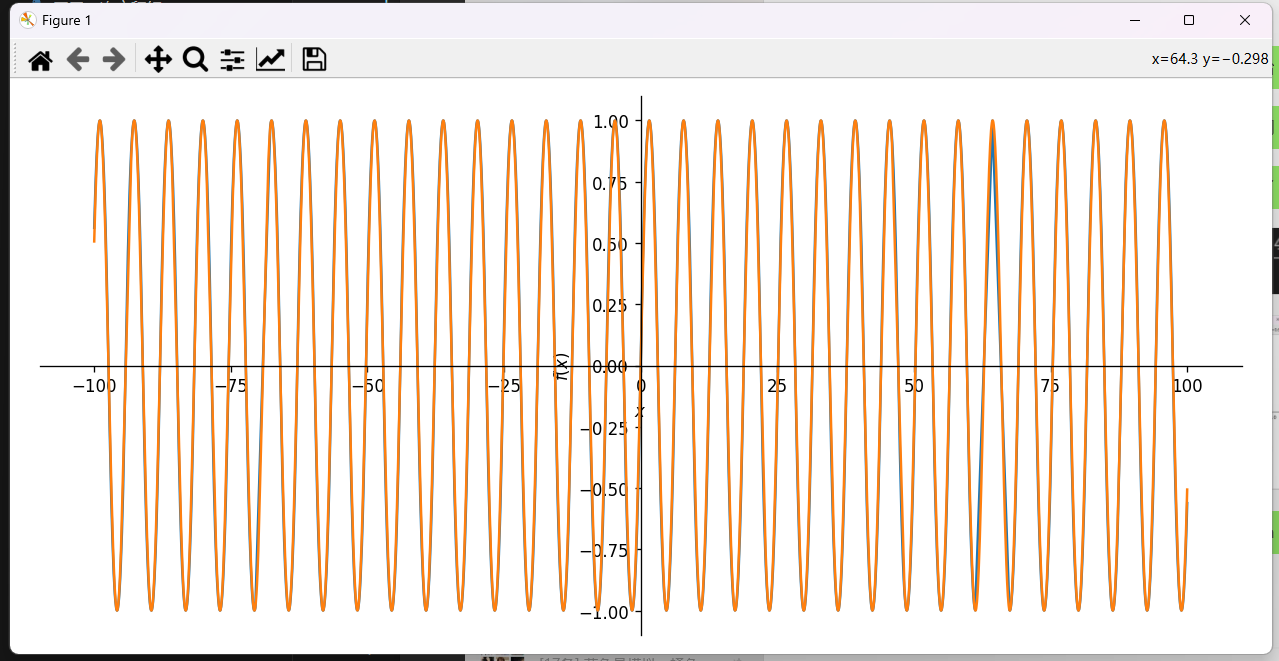
可以看到，这个函数已经有了类似$\sin$函数的效果了，那么理论成立，就开始实践吧！

实际操作

工具准备（可选）

• Python
• sympy库（Python）

正文

首先，想要模拟$\sin$函数，得先有模拟出来的二次函数表达式，但是这个要怎么搞呢？

这里放一张图：

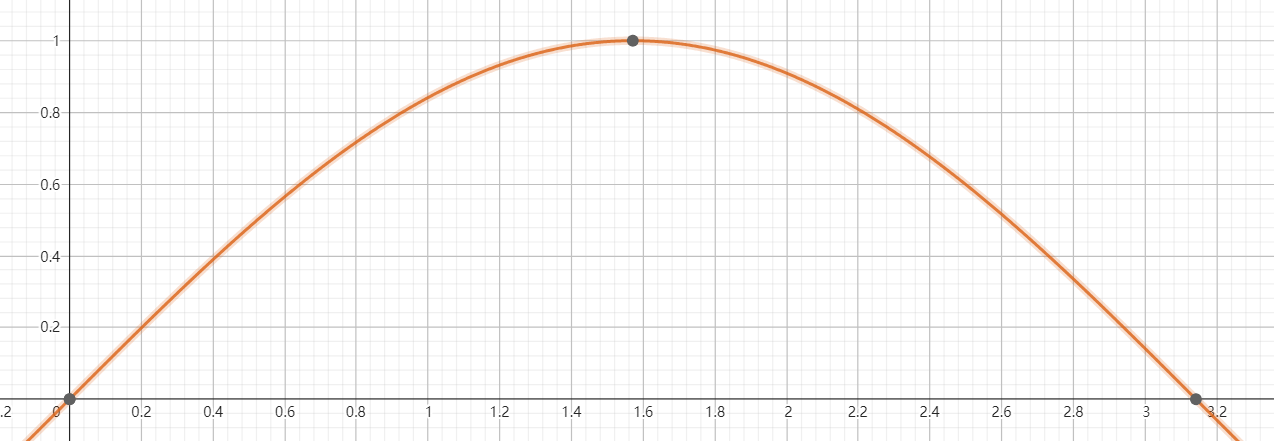
可以看到这张图是$\sin$函数连续的弧中的其中一段弧，图中有三个黑色的点，已知它们的坐标分别为：$(0,0),(\frac\pi2,1),(\pi,0)$

那么我们可以用这三个点把二次函数表达式很方便地用Python的Sympy库求出来:

from sympy import *

a, b, c = symbols('a b c')

l = [(0,0),(Rational(1,2)*pi,1),(pi,0)]
f = []
for i in l:
    f.append(a*(i[0]**2)+b*(i[0])+c-i[1])

print(solve(f, [a, b, c]))

输出内容：

{a: -4/pi**2, b: 4/pi, c: 0}

可以得到：

$$\begin{cases} a=\frac{-4}{\pi^2}\\ b=\frac{4}{\pi}\\ c=0 \end{cases}$$

所以代入二次函数表达式一般形式$f(x)=ax^2+bx+c$可得函数表达式为：

$$f(x)=-\frac4{\pi^2}x+\frac{4}{\pi}x$$

然后根据理论部分的内容对函数进行修改，得出：

$$f(x)=(-1)^{\lfloor\frac x\pi\rfloor}(-\frac{4(x\mod\pi)^2}{\pi^2}+\frac{4(x\mod\pi)}\pi)$$

然后我们再来看看最终效果，画图源代码：

from sympy import *

x = symbols('x')
fp = x%pi
f = (-1)**floor(x/pi)*(-4/pi**2*fp**2+4/pi*fp)
plot(f, sin(x), (x, -10, 10))

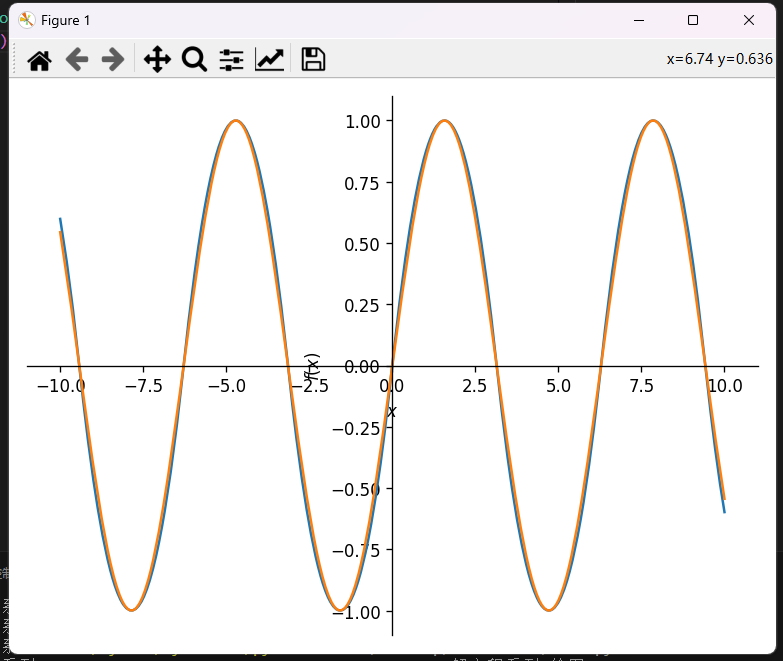
所以这样就完毕了，不过这个函数还是跟$\sin$有很大误差的，内容仅整活🧐